Skip to main content
Evaluation Population evaluation measures how accurately your custom population can predict responses to new questions. This testing process provides confidence metrics that help you understand the reliability of your API predictions.

​
Testing methodologies

Semilattice uses two types of testing to evaluate population model accuracy.

​
Built-in cross-validation

The default testing method uses a population model’s seed data to evaluate its accuracy via leave-one-out cross-validation. For each question in the seed dataset:
  1. The question and all answer data are temporarily removed from the set of data used by the model.
  2. The question is then predicted using the remaining data.
  3. Accuracy scores are calculated by comparing the predicted answer distribution with the held back ground truth distribution.
Once this has been done for all questions in the seed dataset, the accuracy scores are averaged to calculate overall accuracy metrics for the population model.
The API does not support predicting open-ended outputs. If your seed dataset contains open-ended data, these questions will not be tested during cross-validation. Their status will be Not Tested and overall accuracy metrics will be calculated with the results from other questions.

​
User-defined test runs

You can also test population models against sets of ground truth questions which are not part of the seed dataset. This enables use-case specific or periodic benchmarking. See the tests section to learn how to run test predictions.

​
Triggering cross-validation

You can trigger cross-validation tests using the test method: 
# Trigger population testing
response = semilattice.populations.test(population_id="your_population_id")
population = response.data
You need to poll for completion as testing runs asynchronously: 
import time

while population.status != "Tested":
    time.sleep(1)
    response = semilattice.populations.get(population_id=population_id)
    population = response.data

print("Testing complete!")
The status field will progress through:
  1. “Testing”: Population test is currently running
  2. “Tested”: Testing completed successfully, metrics are available
If something goes wrong the status will be “Action Required”, indicating that testing failed due to a simulation error on one or more questions.

​
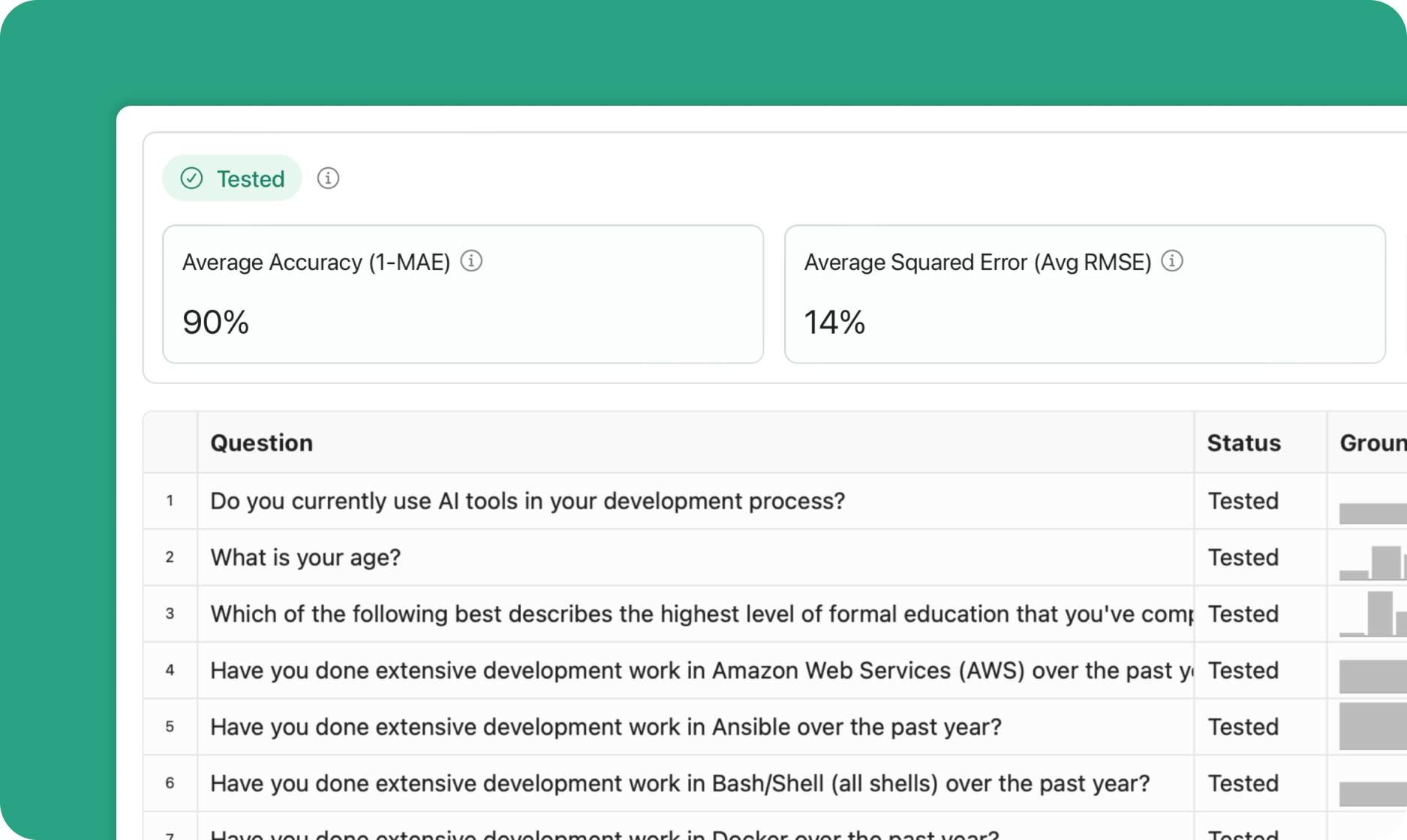
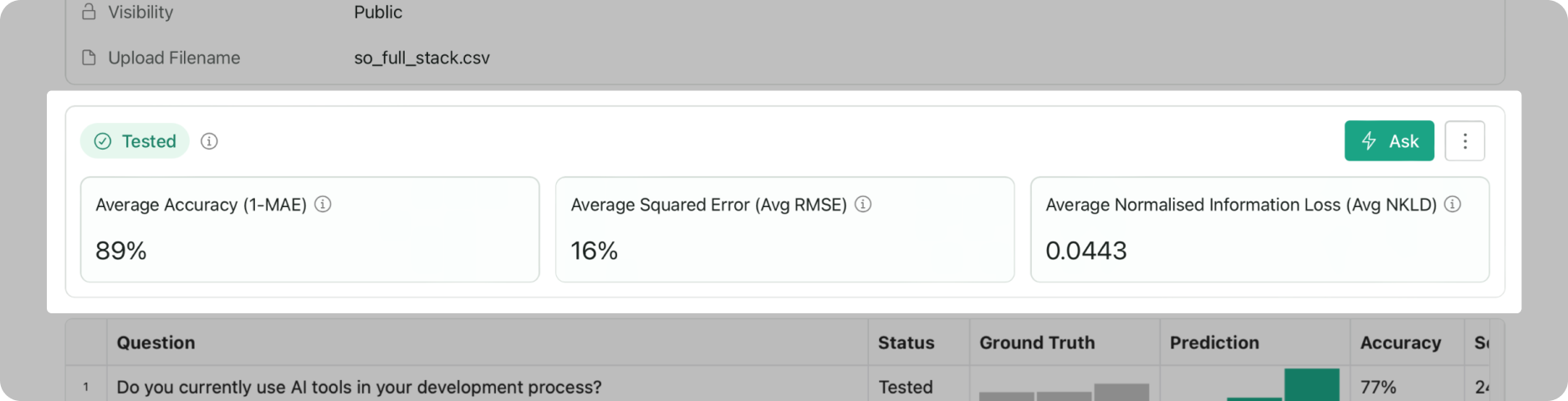
Evaluation metrics

Four key accuracy metrics

For both built-in cross-validation tests and user-defined test batches, the API calculates three accuracy metrics:

​
Average Accuracy

  • Field: average_accuracy
  • Range: 0 to 1 (higher is better)
  • Calculation: The mean absolute error (MAE) between the predicted and ground truth answer distributions for each question is calculated, averaged, and then subtracted from 1 to convert it from an error measure to a crude accuracy measure.
  • Example: 0.8721

​
Average Squared Error

  • Field: average_squared_error
  • Range: 0 to 1 (lower is better)
  • Calculation: The root mean squared error (RMSE) between the predicted and ground truth answer distributions for each question is calculated and then averaged.
  • Example: 0.1607

​
Average Normalised Information Loss

  • Field: average_normalised_information_loss
  • Range: 0 to 1+ (lower is better)
  • Calculation: The Kullback–Leibler (KL) divergence (also called relative entropy) between the predicted and ground truth answer distributions for each question is calculated, normalised to the number of answer options in the question, and then averaged.
  • Example: 0.0063

​
Interpreting results

Based on all of our benchmarking to date, we have some hueristics on what “good” looks like.

​
Good performance thresholds

  • Average Accuracy: Above 0.85 (higher values indicate better accuracy)
  • Average Squared Error: Below 0.18 (lower values indicate more consistent predictions)
  • Average Normalised Information Loss: Below 0.1 (lower values indicate better distribution matching)

​
Benchmarking context

These thresholds come from extensive benchmarking work:
MetricGood ThresholdBenchmarking AverageBenchmarking Range
Average AccuracyAbove 0.850.870.82 - 0.92
Average Squared ErrorBelow 0.180.160.11 - 0.24
Average Normalised Information LossBelow 0.10.05690.0244 - 0.1006
We increasingly find Average Normalised Information Loss to be the best single metric, but usually expect scores across all three metrics to be “good” to consider a population model reliable.

​
Accessing evaluation results

Once testing is complete, metrics are available in API responses: 
# Get population with evaluation metrics
response = semilattice.populations.get(population_id=population_id)
population = response.data

print(f"Average Accuracy: {population.average_accuracy}")
print(f"Average Squared Error: {population.average_squared_error}")
print(f"Average Normalised Information Loss: {population.average_normalised_information_loss}")
⌘I